Математика Биткоина простым языком

В 2024 году Bitcoin оставался драйвером криптовалютного рынка, который задавал направление и темпы роста для остальных монет. С января по декабрь главный цифровой актив вырос в цене более чем на 60% (с $29,08 тыс. до $47,87 тыс.). На пике курс валюты достигал $69 тыс. За год капитализация BTC увеличилась в 1,7 раз (с $543,88 млрд до $924,61 млрд). Причина такой популярности — в совокупности факторов: безопасности, анонимности, отсутствии границ и других. Но главным является математика Биткоина, на которой построена криптовалюта. Благодаря синергии эллиптических кривых и конечных полей система исправно работает.

Основа математики биткоина

Криптовалюта полностью меняет привычное определение собственности. В традиционном мире владеть чем-либо означает распоряжаться его физическим выражением. Блокчейн работает по-другому. Цифровые монеты — это записи в распределенном реестре, которые не имеют физического эквивалента. Владеть биткоином подразумевает распоряжаться им по своему усмотрению, фиксируя транзакции в блокчейне.

Такую способность обеспечивает механизм Elliptic Curve Digital Signature Algorithm. Это система криптографических подписей, построенная на эллиптических кривых и конечных полях. Ее невозможно подделать, а достоверность легко проверяется любым участником сети.

ECDSA включает 2 отдельные процедуры для создания подписи и ее верификации. Каждая представляет собой механизм, сочетающий несколько математических операций. Первая использует приватный ключ, чтобы активировать транзакцию. Вторая проверяет ее посредством открытого набора символов.

Лучшие криптобиржи

Рейтинг

Отзывы

Цена

Объем за 24 ч

BitMart

5.0

65

$ 69 725,01

47 548,23 BTC $ 3,34 млрд

$ 69 725,01

Купить

Bitget

4.9

393

$ 98 169,34

3500,82 BTC $ 343,67 млн

$ 98 169,34

Купить

Bybit

4.9

1020

$ 69 617,18

16 570,79 BTC $ 1,16 млрд

$ 69 617,18

Купить

CoinEx

4.8

201

$ 69 719,99

268,43 BTC $ 18,88 млн

$ 69 719,99

Купить

BYDFi

4.8

5

$ 97 729,12

1291,42 BTC $ 126,21 млн

$ 97 729,12

Купить

все биржи

Эллиптические кривые

Концепция ECDSA была представлена в 1992 году криптографом Скоттом Ванстоуном. Эллиптическая кривая в ней показана отметками на графике, порядок которых можно описать формулой: y2 = x3 + ax + b. В протоколе BTC a принято за 0, а b равно 7. Графически этот элемент выглядит так:

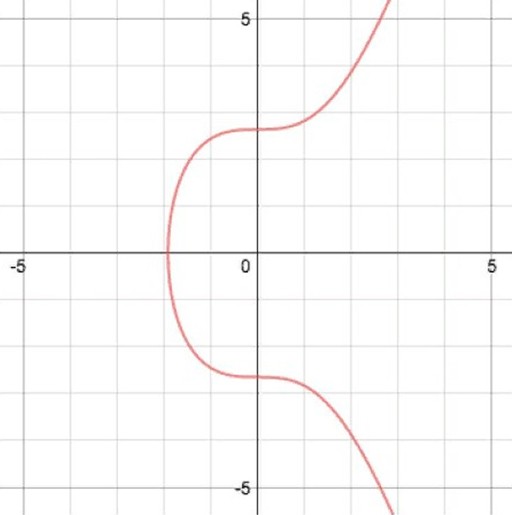
Элемент имеет несколько полезных особенностей:

• Невертикальная линия, проходящая через кривую в 2 точках, обязательно пересечет ее и в 3.
• Если такая прямая касается эллиптического элемента в одном месте, она пройдет через него и в другом.

5 отличий между биткоином и эфириумом

Пройди опрос и получи в подарок скидку на торговую комиссию и книгу о криптовалюте

Пройти опрос

Эти характеристики используют в сложении и удвоении точек. В первом случае через слагаемые P и Q (на графике) нужно провести прямую линию. Она пересечет кривую в точке R′. После этого необходимо найти на эллиптической линии отметку, противоположную по значению R′. Ее можно назвать R и принять за сумму P и Q.

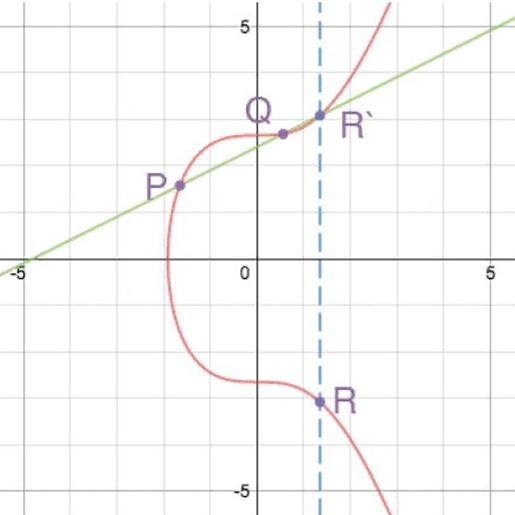
Для удвоения значения используют формулу P + P = R. На графике проводят линию, которая касается кривой на отметке P. Учитывая характеристики элемента, отрезок должен пересечь его в точке R′, противоположной по значению R. В этом случае R принимают за отметку удвоения.

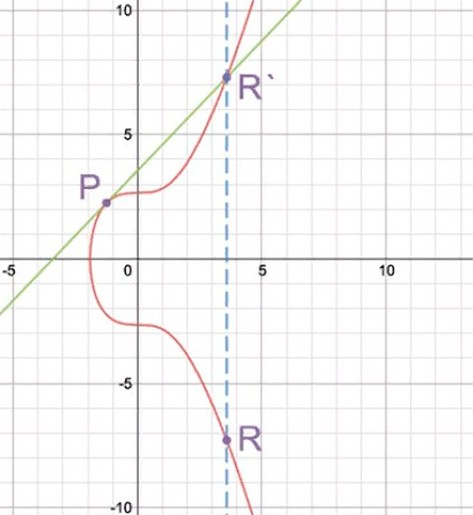
Эти 2 расчета нужны, чтобы определить скалярное произведение R = aP (добавление отметки P к самой себе a количество раз).

Для BTC R = 7P или R = P + (P + (P + (P + (P + P))))).

Если упростить, получится:

R = P + 6P
R = P + 2 (3P)
R = P + 2 (P + 2P).

Таким образом, операцию разделяют на 2 этапа по удвоению отметки и 2 — по сложению. Для работы со сложными числами используют более быстрые способы.

Конечные поля

В криптографии применяют ту же кривую, но рассматривают ее в определенных числовых границах. Это конечное поле, в которое теоретически попадают результаты всех вычислений.

В качестве примера можно определить остаток от деления на целое число (операция modulus — MOD): 9/7 = 1 с остатком 2. Операция имеет значение: 9 MOD 7 = 2. Границы конечного поля — 0 и 6. Это значит, что результаты всех расчетов по модулю 7, независимо от исходного числа, попадут в указанный диапазон.

 Загрузка ...

Эллиптическую кривую Bitcoin по формуле y2 + x3 +7 определяют на конечном поле по модулю 67. На графике это выражено скоплением отметок. Все показатели x и y в них — целые числа в диапазоне 0-66. Прямые линии оборачиваются вокруг выделенного пространства, как только достигнут числа 67, чтобы продолжиться с другой стороны. Если сложить отметки 2, 22 и 6, 25, то проходящая через них линия пересечет третью — 47, 39. Итогом вычисления станет противоположная ей по значению отметка 47, 28.

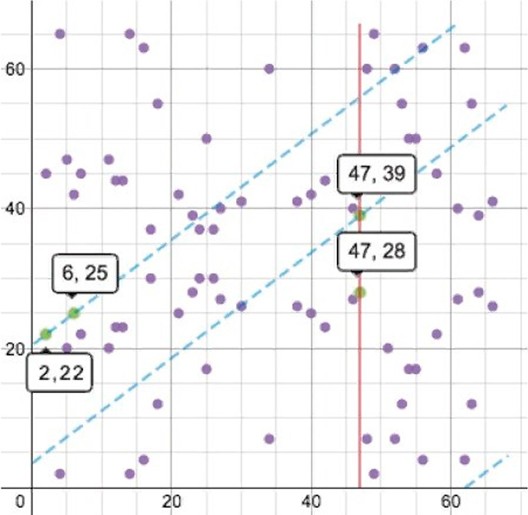
Использование в криптографии

Протокол биткоина фиксирует значения для эллиптической кривой и заданного пространства. Поэтому каждый участник сети может применять только определенные формулы. К фиксированным характеристикам относятся:

• Формула эллиптического элемента (equation).
• Базовая точка (base point).
• Показатель модуля поля (prime modulus).
• Порядок базовой точки (order).

Для этих значений в математике биткоина используются сложные числа. Они обеспечивают безопасность криптовалютной сети, поскольку найти приватный ключ к транзакции или кошельку простым перебором (методом брутфорса) практически невозможно. Расчет значений для BTC представлен в таблице.

Эта последовательность значений называется secp256k1. В протоколе Bitcoin ее используют вместе со схемой ECDSA. Приватный ключ система задает числом между 1 и показателем порядка. Открытый получают из секретного методом склярного умножения на показатель базовой отметки.

Читайте также

Проблемы Биткоина в 2024 году и пути их решения

Bitcoin — главная криптовалюта на рынке виртуальных активов. Некоторые инвесторы уже окрестили ее...

Сколько будет стоить биткоин в 2025 году

Все больше традиционных инвесторов интересуются возможностью вкладывать деньги в криптовалюту. В...

Как можно было купить биткоин в 2009 году

Bitcoin — первая успешная криптовалюта. В ноябре 2021 года монета установила исторический ценовой...

Если слишком сложно

Блокчейн биткоина построен на математических принципах. Для отправки транзакций сеть использует схему цифровых подписей — ECDSA. Механизм работает на основе эллиптических кривых, рассчитанных в определенных числовых рамках. С помощью этих функций создается сложная система генерирования приватных и публичных адресов.

С одной стороны, математический порядок создания цифровой подписи показывает, что максимальное число биткоин-кошельков определено. Но с другой — сложность расчетов увеличивается по экспоненте. Чтобы решить задачу, потребуется около 2¹²⁸ попыток. Это займет количество времени, сопоставимое с существованием Вселенной.

Часто задаваемые вопросы

Заместитель главного редактора

Евгений Лукин